Introduction to Mathematical Functionality

It’s a fact of life, math is hard. Unfortunately, 3D graphics require a fair bit of knowledge about the subject. Fortunately, jME is able to hide the majority of the details away from the user. Vectors are the fundamental type in the 3D environment, and it is used extensively. Matrices are also a basic necessity of 3D for representing linear systems. Quaternions are perhaps the most powerful and complicated of the basic types and are used for rotation in jME.

I’ll discuss how these are used in the system for the core functionality. Including Transforming, Visibility Determination, Collision Detection, and the Coordinate System. Note, that these are low level details. Further chapters will discuss how to use these various systems from a high level perspective.

To get a visual introduction to math in jME3 for the absolute beginner, check out our Math for Dummies introduction class.

Coordinate System

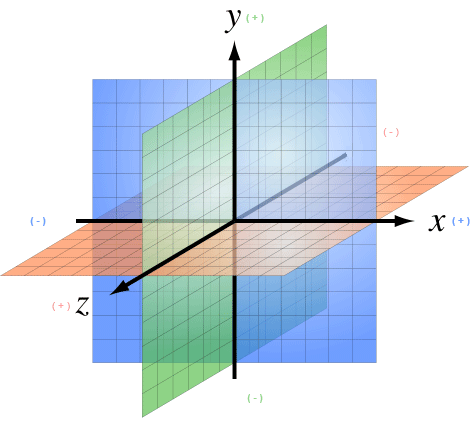
Definition

A coordinate system consists of an origin (single point in space) and three coordinate axes that are each unit length and mutually perpendicular. The axes can be written as the column of a Matrix, R = [U1|U2|U3]. In fact, this is exactly how CameraNode works. The coordinate system defined by Camera is stored in a Matrix.

jME uses a Right-Handed coordinate system (as OpenGL does).

The definition of a coordinate system is defined in jME by the properties sent to Camera. There are no error checks to insure that: 1) the coordinate system is right-handed and 2) The axes are mutually perpendicular. Therefore, if the user sets the axes incorrectly, they are going to experience very odd rendering artifacts (random culling, etc).

coordinate-system.png

Homogenous coordinates

Homogenous coordinates have an additional W value tacked on to the end. The XYZ values are to be divided by W to give the true coordinates.

This has several advantages, one technical, some relevant to application programmers:

Technically, it simplifies some formulae used inside the vector math. For example, some operations need to apply the same factor to the XYZ coordinates. Chain multiple operations of that kind (and vector math tends to do that), and you can save a lot of multiplications by simply keeping the scaling factor around and doing the multiplication to XYZ at the end of the pipeline, in the 3D card (which does accept homogenous coordinates). It also simplifies some formulae, in particular anything that is related to rotations.

For application programmers, this means you can express infinitely long vectors that still have a direction - these tend to be used in lighting. Just use a W value of 0.0.

Transformations

Transformations define an operation that converts points from one coordinate system to another. This includes translation, rotation and scaling. In jME, local transforms are used to represent the positioning of objects relative to a parent coordinate system. While, world transforms are used to represent the positioning of objects in a global coordinate system.

Visibility Determination

Visibility Determination concerns itself with minimizing the amount of data that is sent to the graphics card for rendering. Specifically, we do not want to send data that will not be seen. Data not sent to the graphics card is said to be culled. The primary focus of this section is Frustum Culling based on the Camera’s view frustum. In essence, this frustum creates six standard view planes. The BoundingVolume of an object is tested against the frustum planes to determine if it is contained in the frustum. If at any point the object’s bounding is outside of the plane, it is tossed out and no longer processed for rendering. This also includes any children that it managed, allowing fast culling of large sections of the scene.

Fundamental Types

ColorRGBA

Definition

ColorRGBA defines a color value in the jME library. The color value is made of three components, red, green and blue. A fourth component defines the alpha value (transparent) of the color. Every value is set between [0, 1]. Anything less than 0 will be clamped to 0 and anything greater than 1 will be clamped to 1.

Note: If you would like to “convert” an ordinary RGB value (0-255) to the format used here (0-1), simply multiply it with: 1/255.

jME Class

ColorRGBA defines a few static color values for ease of use. That is, rather than:

ColorRGBA red = new ColorRGBA(1,0,0,1);
object.setSomeColor(red);

you can simply say:

object.setSomeColor(ColorRGBA.red)

ColorRGBA will also handle interpolation between two colors. Given a second color and a value between 0 and 1, a the owning ColorRGBA object will have its color values altered to this new interpolated color.

Matrix

See Matrix3f Javadoc and Matrix4f Javadoc

Definition

A Matrix is typically used as a linear transformation to map vectors to vectors. That is: Y = MX where X is a Vector and M is a Matrix applying any or all transformations (scale, rotate, translate).

There are a few special matrices:

zero matrix is the Matrix with all zero entries.

0 0 0

0

0

0

0

0

0

The Identity Matrix is the matrix with 1 on the diagonal entries and 0 for all other entries.

1 0 0

0

1

0

0

0

1

A Matrix is invertible if there is a matrix M-1 where MM-1 = M-1M = I.

The transpose of a matrix M = [mij] is MT = [mji]. This causes the rows of M to become the columns of MT.

1 1 1 1 2 3

2

2

2

⇒

1

2

3

3

3

3

1

2

3

A Matrix is symmetric if M = MT.

X A B

A

X

C

B

C

X

Where X, A, B, and C equal numbers

jME includes two types of Matrix classes: Matrix3f and Matrix4f. Matrix3f is a 3x3 matrix and is the most commonly used (able to handle scaling and rotating), while Matrix4f is a 4x4 matrix that can also handle translation.

Transformations

Multiplying a vector with a Matrix allows the vector to be transformed. Either rotating, scaling or translating that vector.

Scaling

If a diagonal Matrix, defined by D = [dij] and dij = 0 for i != j, has all positive entries it is a scaling matrix. If di is greater than 1 then the resulting vector will grow, while if di is less than 1 it will shrink.

Rotation

A rotation matrix requires that the transpose and inverse are the same matrix (R-1 = RT). The rotation matrix R can then be calculated as: R = I + (sin(angle)) S + (1 - cos(angle)S2 where S is:

0 u2 -u1

-u2

0

u0

u1

-u0

0

Translation

Translation requires a 4x4 matrix, where the vector (x,y,z) is mapped to (x,y,z,1) for multiplication. The Translation Matrix is then defined as:

M T

ST

1

where M is the 3x3 matrix (containing any rotation/scale information), T is the translation vector and ST is the transpose Vector of T. 1 is just a constant.

jME Class

Both Matrix3f and Matrix4f store their values as floats and are publicly available as (m00, m01, m02, …, mNN) where N is either 2 or 3.

Most methods are straight forward, and I will leave documentation to the Javadoc.

Vector

See Vector3f Javadoc and Vector2f Javadoc

Definition

Vectors are used to represent a multitude of things in jME, points in space, vertices in a triangle mesh, normals, etc. These classes (Vector3f in particular) are probably the most used class in jME.

A Vector is defined by an n-tuple of real numbers. V = <V1, V2,…, Vn>.

We have two Vectors (2f and 3f) meaning we have tuples of 2 float values or 3 float values.

Operations

Multiplication by Scalar

A Vector can be multiplied by a scalar value to produce a second Vector with the same proportions as the first. aV = Va = <aV1, aV2,…,aVn>

Addition and Subtraction

Adding or subtracting two Vectors occurs component-wise. That is the first component is added (subtracted) with the first component of the second Vector and so on.

P + Q = <P1+Q1, P2+Q2, …, Pn+Qn>

Magnitude

The magnitude defines the length of a Vector. A Vector of magnitude 1 is unit length.

For example, if V = (x, y, z), the magnitude is the square root of (x2 + y2 + z2).

A Vector can be normalized or made unit length by multiplying the Vector by (1/magnitude).

Dot Products

The dot product of two vectors is defined as: P dot Q = PxQx + PyQy + PzQz

Using the dot product allows us to determine how closely two Vectors are pointing to the same point. If the dot product is negative they are facing in relatively opposite directions, while positive tells us they are pointing in the relative same direction.

If the dot product is 0 then the two Vectors are orthogonal or 90 degrees off.

Cross Product

The Cross Product of two Vectors returns a third Vector that is perpendicular to the two Vectors. This is very useful for calculating surface normals.

P X Q = <PyQz - PzQy, PzQx - PxQz, PxQy - PyQx>

jME Class

Vector3f and Vector2f store their values (x, y, z) and (x, y) respectively as floats. Most methods are straight forward, and I will leave documentation to the Javadoc.

Quaternion

See Quaternion Javadoc

Definition

Quaternions define a subset of a hypercomplex number system. Quaternions are defined by (i2 = j2 = k2 = ijk = -1). jME makes use of Quaternions because they allow for compact representations of rotations, or correspondingly, orientations, in 3D space. With only four float values, we can represent an object’s orientation, where a rotation matrix would require nine. They also require fewer arithmetic operations for concatenation.

Additional benefits of the Quaternion is reducing the chance of Gimbal Lock and allowing for easily interpolation between two rotations (spherical linear interpolation or slerp).

While Quaternions are quite difficult to fully understand, there are an exceeding number of convenience methods to allow you to use them without having to understand the math behind it. Basically, these methods involve nothing more than setting the Quaternion’s x,y,z,w values using other means of representing rotations. The Quaternion is then contained in the Spatial as its local rotation component.

Quaternion q has the form

q = <_w,x,y,z_> = w + xi + yj + zk

or alternatively, it can be written as:

q = s + v, where s represents the scalar part corresponding to the w-component of q, and v represents the vector part of the (x, y, z) components of q.

Multiplication of Quaternions uses the distributive law and adheres to the following rules with multiplying the imaginary components (i, j, k):

i2 = j2 = k2 = -1+ ij = -ji = k+ jk = -kj = i+ ki = -ik = j

However, Quaternion multiplication is not commutative, so we have to pay attention to order.

q1q2 = s1s2 - v1 dot v2 + s1v2 + s2v1 + v1 X v2

Quaternions also have conjugates where the conjugate of q is (s - v)

These basic operations allow us to convert various rotation representations to Quaternions.

Angle Axis

You might wish to represent your rotations as Angle Axis pairs. That is, you define a axis of rotation and the angle with which to rotate about this axis. Quaternions defines a method fromAngleAxis (and fromAngleNormalAxis) to create a Quaternion from this pair. This is actually used quite a bit in jME demos to continually rotate objects. You can also obtain a Angle Axis rotation from an existing Quaternion using toAngleAxis.

Example - Rotate a Spatial Using fromAngleAxis

//rotate about the Y-Axis by approximately 1 pi
Vector3f axis = Vector3f.UNIT_Y;
// UNIT_Y equals (0,1,0) and does not require to create a new object
float angle = 3.14f;
s.getLocalRotation().fromAngleAxis(angle, axis);

Three Angles

You can also represent a rotation by defining three angles. The angles represent the rotation about the individual axes. Passing in a three-element array of floats defines the angles where the first element is X, second Y and third is Z. The method provided by Quaternion is fromAngles and can also fill an array using toAngles

Example - Rotate a Spatial Using fromAngles

//rotate 1 radian on the x, 3 on the y and 0 on z
float[] angles = {1, 3, 0};
s.getLocalRotation().fromAngles(angles);

Three Axes

If you have three axes that define your rotation, where the axes define the left axis, up axis and directional axis respectively) you can make use of fromAxes to generate the Quaternion. It should be noted that this will generate a new Matrix object that is then garbage collected, thus, this method should not be used if it will be called many times. Again, toAxes will populate a Vector3f array.

Example - Rotate a Spatial Using fromAxes

//rotate a spatial to face up ~45 degrees
Vector3f[] axes = new Vector3f[3];
axes[0] = new Vector3f(-1, 0, 0); //left
axes[1] = new Vector3f(0, 0.5f, 0.5f); //up
axes[2] = new Vector3f(0, 0.5f, 0.5f); //dir

s.getLocalRotation().fromAxes(axes);

Rotation Matrix

Commonly you might find yourself with a Matrix defining a rotation. In fact, it’s very common to contain a rotation in a Matrix, create a Quaternion, rotate the Quaternion, and then get the Matrix back. Quaternion contains a fromRotationMatrix method that will create the appropriate Quaternion based on the given Matrix. The toRotationMatrix will populate a given Matrix.

Example - Rotate a Spatial Using a Rotation Matrix

Matrix3f mat = new Matrix3f();
mat.setColumn(0, new Vector3f(1,0,0));
mat.setColumn(1, new Vector3f(0,-1,0));
mat.setColumn(2, new Vector3f(0,0,1));

s.getLocalRotation().fromRotationMatrix(mat);

As you can see there are many ways to build a Quaternion. This allows you to work with rotations in a way that is conceptually easier to picture, but still build Quaternions for internal representation.

Slerp

One of the biggest advantages to using Quaternions is allowing interpolation between two rotations. That is, if you have an initial Quaternion representing the original orientation of an object, and you have a final Quaternion representing the orientation you want the object to face, you can do this very smoothly with slerp. Simply supply the time, where time is [0, 1] and 0 is the initial rotation and 1 is the final rotation.

Example - Use Slerp to Rotate Between two Quaternions

/*
You can interpolate rotations between two quaternions using spherical linear
interpolation (slerp).
*/
Quaternion Xroll45 = new Quaternion();
Xroll45.fromAngleAxis(45 * FastMath.DEG_TO_RAD, Vector3f.UNIT_X);
//
Quaternion Yroll45 = new Quaternion();
Yroll45.fromAngleAxis(45 * FastMath.DEG_TO_RAD, Vector3f.UNIT_Y);

//the rotation half - way between these two

Quaternion halfBetweenXroll45Yroll45 = new Quaternion();
halfBetweenXroll45Yroll45.slerp(Xroll45, Yroll45, 0.5f);
geom2.setLocalRotation(halfBetweenXroll45Yroll45);

Multiplication

You can concatenate (add) rotations: This means you turn the object first around one axis, then around the other, in one step.

Quaternion myRotation = pitch90.mult(roll45); /* pitch and roll */

To rotate a Vector3f around its origin by the Quaternion amount, use the multLocal method of the Quaternion:

Quaternion myRotation = pitch90;
Vector3f myVector = new Vector3f(0,0,-1);
myRotation.multLocal(myVector);

Utility Classes

Along with the base Math classes, jME provides a number of Math classes to make development easier (and, hopefully, faster). Most of these classes find uses throughout the jME system internally. They can also prove beneficial to users as well.

Fast Math

See FastMath Javadoc

Definition

FastMath provides a number of convenience methods, and where possible faster versions (although this can be at the sake of accuracy).

Usage

FastMath provides a number of constants that can help with general math equations. One important attribute is USE_FAST_TRIG if you set this to true, a look-up table will be used for trig functions rather than Java’s standard Math library. This provides significant speed increases, but might suffer from accuracy so care should be taken.

There are five major categories of functions that FastMath provides.

Trig Functions

  • cos and acos - provide cosine and arc cosine values (make use of the look-up table if USE_FAST_TRIG is true)

  • sin and asin - provide sine and arc sine values (make use of the look-up table if USE_FAST_TRIG is true)

  • tan and atan - provide tangent and arc tangent values

Numerical Methods

  • ceil - provides the ceiling (smallest value that is greater than or equal to a given value and an integer)of a value.

  • floor - provides the floor (largest value that is less than or equal to a given value and an integer) of a value.

  • exp - provides the euler number (e) raised to the provided value.

  • sqr - provides the square of a value (i.e. value * value).

  • pow - provides the first given number raised to the second.

  • isPowerOfTwo - provides a boolean if a value is a power of two or not (e.g. 32, 64, 4).

  • abs - provides the absolute value of a given number.

  • sign - provides the sign of a value (1 if positive, -1 if negative, 0 if 0).

  • log - provides the natural logarithm of a value.

  • sqrt - provides the square root of a value.

  • invSqrt - provides the inverse square root of a value (1 / sqrt(value).

Linear Algebra

Geometric Functions

  • counterClockwise - given three points (defining a triangle), the winding is determined. 1 if counter-clockwise, -1 if clockwise and 0 if the points define a line.

  • pointInsideTriangle - calculates if a point is inside a triangle.

  • sphericalToCartesian - converts a point from spherical coordinates to Cartesian coordinates.

  • cartesianToSpherical - converts a point from Cartesian coordinates to spherical coordinates.

Misc.

  • nextRandomFloat - obtains a random float.

Line

See Line Javadoc

Definition

A line is a straight one-dimensional figure having no thickness and extending infinitely in both directions. A line is defined by two points A and B with the line passing through both.

Usage

jME defines a Line class that is defined by an origin and direction. In reality, this Line class is typically used as a line segment. Where the line is finite and contained between these two points.

random provides a means of generate a random point that falls on the line between the origin and direction points.

Example 1 - Find a Random Point on a Line

Line l = new Line(new Vector3f(0,1,0), new Vector3f(3,2,1));
Vector3f randomPoint = l.random();

Plane

See Plane Javadoc

Definition

A plane is defined by the equation N . (X - X0) = 0 where N = (a, b, c) and passes through the point X0 = (x0, y0, z0). X defines another point on this plane (x, y, z).

N . (X - X0) = 0 can be described as (N . X) + (N . -X0) = 0

or

(ax + by + cz) + (-ax0-by0-cz0) = 0

where (-ax0-by0-cz0) = d

Where d is the negative value of a point in the plane times the unit vector describing the orientation of the plane.

This gives us the general equation: (ax + by + cz + d = 0)

Usage in jME

jME defines the Plane as ax + by + cz = -d. Therefore, during creation of the plane, the normal of the plane (a,b,c) and the constant d is supplied.

The most common usage of Plane is Camera frustum planes. Therefore, the primary purpose of Plane is to determine if a point is on the positive side, negative side, or intersecting a plane.

Plane defines the constants:

  • NEGATIVE_SIDE - represents a point on the opposite side to which the normal points.

  • NO_SIDE - represents a point that lays on the plane itself.

  • POSITIVE_SIDE - represents a point on the side to which the normal points.

These values are returned on a call to whichSide.

Example 1 - Determining if a Point is On the Positive Side of a Plane

Vector3f normal = new Vector3f(0,1,0);
float constant = new Vector3f(1,1,1).dot(normal);
Plane testPlane = new Plane(normal, constant);

int side = testPlane.whichSide(new Vector3f(2,1,0));

if(side == Plane.NO_SIDE) {
   System.out.println("This point lies on the plane");
}

Example 2 - For the Layperson

Using the standard constructor Plane(Vector3f normal, float constant), here is what you need to do to create a plane, and then use it to check which side of the plane a point is on.

package test;

import java.util.logging.Logger;

import com.jme.math.*;

/**
 *@author Nick Wiggill
 */

public class TestPlanes
{
  public static final Logger logger = Logger.getLogger(LevelGraphBuilder.class.getName());

  public static void main(String[] args) throws Exception
  {
    //***Outline.
    //This example shows how to construct a plane representation using
    //com.jme.math.Plane.
    //We will create a very simple, easily-imagined 3D plane. It will
    //be perpendicular to the x axis (it's facing). It's "centre" (if
    //such a thing exists in an infinite plane) will be positioned 1
    //unit along the positive x axis.

    //***Step 1.
    //The vector that represents the normal to the plane, in 3D space.
    //Imagine a vector coming out of the origin in this direction.
    //There is no displacement yet (see Step 2, below).
    Vector3f normal = new Vector3f(5f,0,0);

    //***Step 2.
    //This is our displacement vector. The plane remains facing in the
    //direction we've specified using the normal above, but now we are
    //are actually giving it a position other than the origin.
    //We will use this displacement to define the variable "constant"
    //needed to construct the plane. (see step 3)
    Vector3f displacement = Vector3f.UNIT_X;
    //or
    //Vector3f displacement = new Vector3f(1f, 0, 0);

    //***Step 3.
    //Here we generate the constant needed to define any plane. This
    //is semi-arcane, don't let it worry you. All you need to
    //do is use this same formula every time.
    float constant = displacement.dot(normal);

    //***Step 4.
    //Finally, construct the plane using the data you have assembled.
    Plane plane = new Plane(normal, constant);

    //***Some tests.
    logger.info("Plane info: "+plane.toString()); //trace our plane's information

    Vector3f p1  = new Vector3f(1.1f,0,0); //beyond the plane (further from origin than plane)
    Vector3f p2  = new Vector3f(0.9f,0,0); //before the plane (closer to origin than plane)
    Vector3f p3  = new Vector3f(1f,0,0); //on the plane

    logger.info("p1 position relative to plane is "+plane.whichSide(p1)); //outputs NEGATIVE
    logger.info("p2 position relative to plane is "+plane.whichSide(p2)); //outputs POSITIVE
    logger.info("p3 position relative to plane is "+plane.whichSide(p3)); //outputs NONE
  }
}

Ray

See Ray Javadoc

Definition

Ray defines a line that starts at a point A and continues in a direction through B into infinity.

This Ray is used extensively in jME for Picking. A Ray is cast from a point in screen space into the scene. Intersections are found and returned. To create a ray supply the object with two points, where the first point is the origin.

Example 1 - Create a Ray That Represents Where the Camera is Looking

Ray ray = new Ray(cam.getLocation(), cam.getDirection());

Rectangle

See Rectangle Javadoc

Definition

Rectangle defines a finite plane within three dimensional space that is specified via three points (A, B, C). These three points define a triangle with the forth point defining the rectangle ( (B + C) - A ).

jME Usage

Rectangle is a straight forward data class that simply maintains values that defines a Rectangle in 3D space. One interesting use is the random method that will create a random point on the Rectangle. The Particle System makes use of this to define an area that generates Particles.

Example 1 : Define a Rectangle and Get a Point From It

Vector3f v1 = new Vector3f(1,0,0);
Vector3f v2 = new Vector3f(1,1,0);
Vector3f v3 = new Vector3f(0,1,0);
Rectangle r = new Rectangle(v1, v2, v3);
Vector3f point = r.random();

Triangle

See Triangle Javadoc

Definition

A triangle is a 3-sided polygon. Every triangle has three sides and three angles, some of which may be the same. If the triangle is a right triangle (one angle being 90 degrees), the side opposite the 90 degree angle is the hypotenuse, while the other two sides are the legs. All triangles are convex and bicentric.

Usage

jME’s Triangle class is a simple data class. It contains three Vector3f objects that represent the three points of the triangle. These can be retrieved via the get method. The get method, obtains the point based on the index provided. Similarly, the values can be set via the set method.

Example 1 - Creating a Triangle

//the three points that make up the triangle
Vector3f p1 = new Vector3f(0,1,0);
Vector3f p2 = new Vector3f(1,1,0);
Vector3f p3 = new Vector3f(0,1,1);
Triangle t = new Triangle(p1, p2, p3);

Tips and Tricks

How do I get height/width of a spatial?

Cast the spatial to com.jme3.bounding.BoundingBox to be able to use getExtent().

Vector3f extent = ((BoundingBox) spatial.getWorldBound()).getExtent(new Vector3f());
float x = ( (BoundingBox)spatial.getWorldBound()).getXExtent();
float y = ( (BoundingBox)spatial.getWorldBound()).getYExtent();
float z = ( (BoundingBox)spatial.getWorldBound()).getZExtent();

How do I position the center of a Geometry?

geo.center().move(pos);